Does the mind play dice?
An experiment with random numbers
Randomness is an awkward concept. Most people have some intuitive idea of what it is supposed to mean, but it’s too intangible for us to feel comfortable with. Worse, randomness is often conflated with arbitrariness, a distasteful and unsettling quality which we usually strive to avoid. Scientists are not immune to this discomfort, either: Einstein famously found quantum theory unpalatable because of the heavy involvement of randomness in its description of the world. “God”, he famously remarked, “does not play dice”.
And yet randomness is important. Outside the realm of quantum mechanics, random numbers underpin the security algorithms that let you shop online without worrying about having your credit card details intercepted and stolen. If you play a lottery or raffle, you expect the numbers to be chosen at random so that everyone has a fair chance of winning.
Actually generating random numbers is not something that people are particularly well equipped for, however. Both simple experiments and full scientific studies have consistently identified biases in individual numbers or sequences generated by humans. But I was curious to try a quick experiment of my own, investigating how people deal with trying to generate random numbers under different degrees of guidance. So I cobbled together an online survey containing the following three questions and posted the link on Facebook and Twitter.
Q1. Please give three random numbers.
Q2. Please give three random numbers between 0 and 1000.
Q3. Please give three random numbers which you think no-one else will give.
By the end of the day I had 48 complete responses from my friends and colleagues, by no means a representative sample of the population at large, but useful, I hoped, to get some idea of how people tackle the problem.
The first and third questions are deliberately open-ended. Any number is a reasonable answer, and that includes negative, fractional, and even complex numbers. The spectrum of all possible numbers is vast—in fact, of course, it is infinite. But overwhelmingly, when faced with these simple questions, people give relatively small, positive whole numbers. Amongst the 144 numbers given in answer to Q1, just two were below zero, and a further five contained a decimal point. The numbers 3 and 7 were chosen no fewer than ten times each, and 1 was chosen nine times. Jointly, the single-digit numbers 0 to 9 accounted for almost a third of all responses, and well over ninety percent of responses had less than ten digits. This is shown in the graph below.
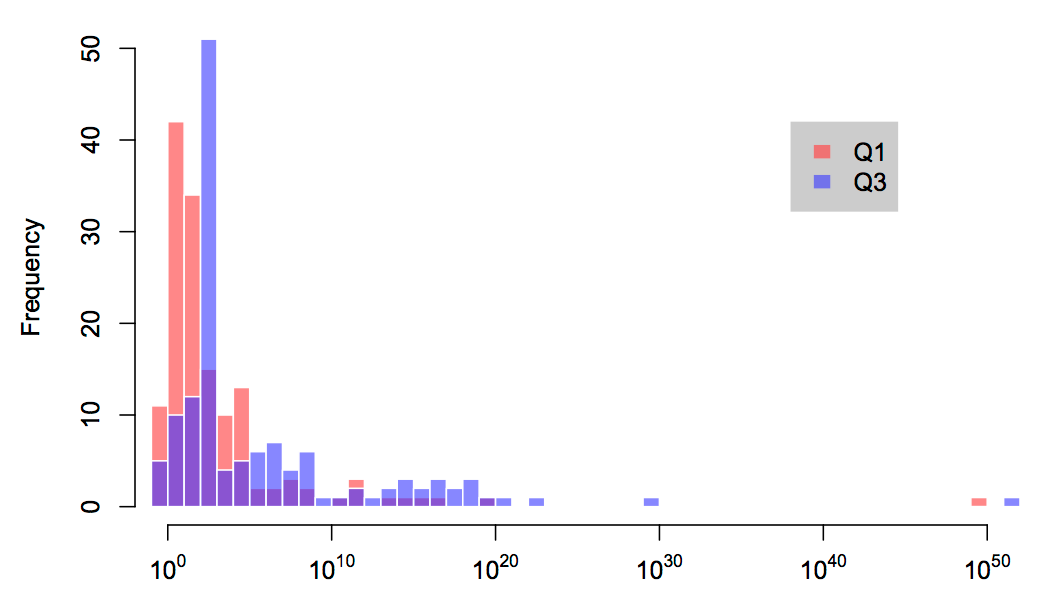
What makes the trend towards small numbers remarkable is that it is the complete opposite of what would be expected from a truly random sample. There are only ten whole numbers with one digit (including zero), making them extraordinarily rare in the grand scheme of things; only a hundred with two or less digits, making them only slightly less scarce; and so on. In other words, large numbers “should” be the norm. In Q3 people were asked to give numbers which they thought no-one else would give. As I expected, and quite appropriately, respondents tended to give larger numbers in this case, in recognition of the fact that this increases the pool of possibilities and makes clashes with others’ choices less likely. The median—the middle value when the numbers are arranged in order—increased 20-fold from 33 to 702, and the number of duplicated values duly dropped from 33 percent to 7 percent.
The fact is that we are simply not used to thinking about and dealing with large numbers, because we don’t come across numbers on this scale regularly in our daily lives. Likewise, whole numbers are far more familiar and useful in day-to-day situations than fractions or the rather abstract negative numbers, and so these are the first to come to mind.
Having said that, fixing the range of numbers of interest changes things substantially. My second question did that, and in the process forced people to override the effects of everyday familiarity with a more mathematical abstraction. In this case, numbers were chosen reasonably evenly, albeit still with a significant bias towards numbers at the extremes of the range.
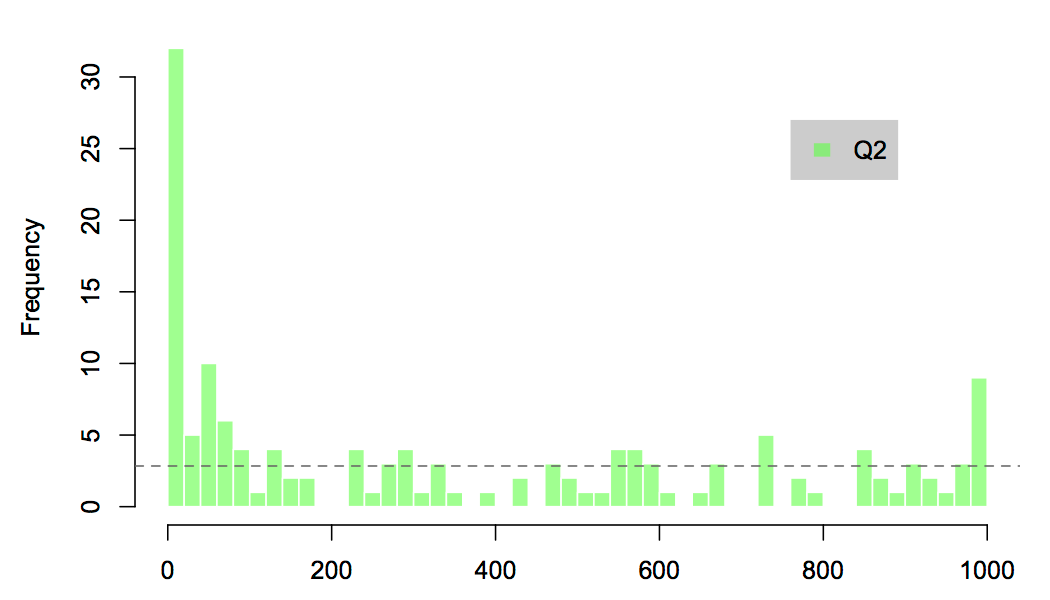
In this case there is a theoretical distribution for truly random numbers, which is shown as a dashed line in the plot. A bit of maths tells us that we would expect an average of nine or ten duplicates in a sample of the size that we have, if they were drawn from this distribution. But the actual number of duplications was 31, more than three times the expected number. So, once again, people are far more predictable in their choices than a random process would be.
In common with other similar experiments, then, we must conclude from this that humans are not good with randomness. But why not? I think the explanation is largely to do with what our brains are adapted for. Most of the time, the brain’s job is to find patterns and order amid the varied and unpredictable information it receives. It is so good at this that we often see patterns where they don’t really exist, a fact that optical illusions and psychological tricksters exploit. So when asked to generate numbers we unconsciously draw on our experience and expectations. It seems the mind doesn’t play dice either. Einstein would have approved.